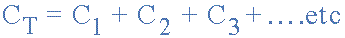KIRCHOFF'S LAW

FIRST LAW

• KCL

Kirchoff's Current Law

-the sum of current entering the node

is equal to the current leaving the node

 

NODE????

- when two or more branches 

 is connected to each other

 BRANCH????

-has a single element 

with each terminals 

 

SECOND LAW

• KVL

Kirchoff's Voltage Law

-states that the sum of voltages in a loop

is always equal zero

LOOP????

 - is any continuous path available 

for current flow from a given point in a circuit and 

back to that same point in the circuit from the 

opposite direction that it left from without 

crossing or retracing 

it`s own path.

 

LEARNINGS:

 

For getting the current I3 in the circuit

using KCL process, you must add the current 

that enters the node and subtract the current that 

leaving the node, then equal to zero. 

OHM'S LAW

- states that the current through a conductor between two points is directly proportional to the potential difference across the two points.

 Types of Element:

• PASSIVE 

- is an electrical component that does not generate power, 

but instead dissipates, stores, and/or releases it.

• ACTIVE

- generate energy.

Short circuit

- that allows a current to travel along 

an unintended path.

 Open circuit

- it lacks a complete path between the 

terminals of its power source

 

LEARNING'S:

You can see to this picture that when the voltage is bigger,

the current will also become bigger.

 And when the resistance of the resistor is big, 

the current will decrease.

 

But, when the resistance of the resistor is small, 

the current that enters the resistor will be bigger.

Therefore, as we change the value of the voltage

and the resistance of the resistor,

the current also change.

• VOLTAGE

- is the FORCE

•  CURRENT

- is the MOTION

• RESISTOR

- is the FRICTION

Introduction of Electric Circuit

This includes the definition of various electrical quantities and their relationships.  

CHARGE(q)
CURRENT(i)
POWER(p) 

CHARGE(q)

    - is the physical property of matter that causes it to experience a force when placed in an   electromagnetic field.

    - The symbol Q is often used to denote a charge.

    - The unit of electric charge is the coulomb(c).

Two types of electric charges
 positive(+) charge
 negative(-) charge 

POSITIVE CHARGE(+)

    - having a deficiency of electrons.
    - having higher electric potential.

NEGATIVE CHARGE(-)

    - a charge that has more electrons than protons and has a lower electrical potential.

Formula for getting charge

q = ʃ idt

 

CURRENT(i)

    - is a flow of electric charge.

    - In electric circuits this charge is often carried by moving electrons in a wire.

    - unit for measuring an electric current is the ampere.

Formula for getting current

i = dq/dt

   POWER(p)

    - the rate at which electrical energy is transferred by a circuit.

                

Capacitor and Inductor

Capacitor

 

-(originally known as a condenser)

 is a passive two-terminal electrical component used to store

energ electro-statically in an electric field.

Consider this is a circuit:

1.  For Computing the Capacitor equivalet

• IN PARALLEL

• IN SERIES

Inductor

-also called a coil or reactor, is a passive two-terminal electrical component which resists changes in electric current passing through it. It consists of a conductor such as a wire, usually wound into a coil. When a current flows through it, energy is stored temporarily in a magnetic field in the coil.

THEVENIN THEOREM AND NORTON EQUIVALENT

Thevinen

-Any linear electrical network with voltage and current sources and only resistances can be replaced at terminals A-B by an equivalent voltage source V_th in series connection with an equivalent resistance R_th.

Norton

- Consist of a single current source and a single parallel resistor.

• For the Thevinen equivalent voltage

• For the Norton equivalent current

MESH ANALYSIS

MESH ANALYSIS

- it is a technique which relies on KVL.

Consider this is a circuit, with two meshes 1 and 2

•  Next, assume current flow clockwise(CW) for easier. 
• Define two mesh current I1 and I2. 
•  Then, assign voltage polarities to all resistor.
• Use KVL in loop 1 and 2 to get the equation.
•  But, in R3 there are two current flow I1 and I2
• So, we write it in this manner -R3(I1-I2) for loop one and for loop two - R3(I2-I1)
• Loop 1 equation: 3 - R1I1 - R3(I1-I2) = 0
• For Loop 2 equation: 10 - R3(I2-I1) - R2I2 = 0
• We can now substitute the value of the resistors, and expand it.

• Use MATRIX to find the value of I1, I2

• For I3, you may use KCL from this node:
  

I1 = I3 + I2

I3 = I1 - I2

I3 = 2 - 3

I3 = -1 mA

WYE - DELTA / DELTA - WYE TRANSFORMATION

WYE - DELTA TRANSFORMATION

- is a mathematical technique to simplify

the analysis electrical network.

Can be used to eliminate one node at a time

and produce a network that can be further simplified, as shown

DELTA - WYE TRANSFORMATION

- is a reverse transformation, which add a node

NODAL ANALYSIS

Node Analysis

- is well organized technique which relies on KCL.

Consider this is a circuit:

The 3 volts source which is connected in the reference and

non-reference node is Node A. Then, the -10 volts source

which is in node C.

Node A = 3V

Node C = -10V

But, when the voltage source is not connected in

reference node it is a SUPER-NODE.

Only Node B is unknown. So, by KCL

we can now get the equation by the sum of current entering

the node is equal to the current leaving the node.

I1 = I2 + I3

By Ohm's Law,

Then, we can now substitute the equation we get from

 OHM'S LAW to the equation we get from KCL.

For solving the current, we use ohm's law,

substitute the voltage in this equation.

I1 = 2 mA

I2 = 3 mA

I3 = -1mA

SERIES AND PARALLEL

SERIES

-only having one path

 for the charges

Consider Circuit A with two resistor

R1 and R2 connected in series:

By KVL 

VT = V1 + V2

Or 

 VT = IR1 + IR2

And, consider an equivalent

Circuit B with one resistor RT:

By Ohm's Law

VT = IRT

But for equivalent circuits, I is the same

for circuit A and circuit B.

   Thus 

VT = IR1 + IR2 = IRT

  Yielding 

R1 + R2 = RT

So, the equivalent total resistance for

resistor in  series is simply the

sum of the individual resistors. 

RT = R1 + R2 + R3 + . . . . . . . RN 

Also note from circuit A that:

 V2 = IR2

I = VT/RT

Thus V2 = VT(R2)/RT 

Where RT = R1 + R2

 

  

This is called the VOLTAGE DIVIDER RULE

Usually written:

VX = VT(RX)/RT

 

 PARALLEL

- from having multiple paths

for current to flow through

 so, the total equivalent resistance 

of the resistors in parallel 

connection

is:

NOTE:

I2 = V/R2

V = ITRT

Thus I2 = IT(RT)/R2

Where 1/RT = 1/R1 + 1/R2

This is called the CURRENT 

DIVIDER RULE  

Usually written:

IX = IT(RT)/RX  

 

AC Circuits

Direct current (DC) circuits involve current flowing in one direction. In alternating current (AC) circuits, instead of a constant voltage supplied by a battery, the voltage oscillates in a sine wave pattern, varying with time as:


V = Vo sin wt

In a household circuit, the frequency is 60 Hz. The angular frequency is related to the frequency, f, by:

w = 2πf

Vo represents the maximum voltage, which in a household circuit in North America is about 170 volts. We talk of a household voltage of 120 volts, though; this number is a kind of average value of the voltage. The particular averaging method used is something called root mean square (square the voltage to make everything positive, find the average, take the square root), or rms. Voltages and currents for AC circuits are generally expressed as rms values. For a sine wave, the relationship between the peak and the rms average is:
rms value = 0.707 peak value

Resistance

The relationship V = IR applies for resistors in an AC circuit, so

I = V/R = (Vo / R) sin(ωt) = Io sin(ωt)

In AC circuits we'll talk a lot about the phase of the current relative to the voltage. In a circuit which only involves resistors, the current and voltage are in phase with each other, which means that the peak voltage is reached at the same instant as peak current. In circuits which have capacitors and inductors (coils) the phase relationships will be quite different.

Resistance is essentially friction against the motion of electrons. It is present in all conductors to some extent (except superconductors!), most notably in resistors. When alternating current goes through a resistance, a voltage drop is produced that is in-phase with the current. Resistance is mathematically symbolized by the letter “R” and is measured in the unit of ohms (Ω). 

Impedance And Reactance

The ratio of voltage to current in a resistor is its resistance. Resistance does not depend on frequency, and in resistors the two are in phase.

 

 

In general, the ratio of voltage to current does depend on frequency and in general there is a phase difference. So impedance is the general name we give to the ratio of voltage to current. It has the symbol Z. Resistance is a special case of impedance. Another special case is that in which the voltage and current are out of phase by 90°: this is an important case because when this happens, no power is lost in the circuit. In this case where the voltage and current are out of phase by 90°, the ratio of voltage to current is called the reactance, and it has the symbol X.

Reactance is essentially inertia against the motion of electrons. It is present anywhere electric or magnetic fields are developed in proportion to applied voltage or current, respectively; but most notably in capacitors and inductors. When alternating current goes through a pure reactance, a voltage drop is produced that is 90^o out of phase with the current. Reactance is mathematically symbolized by the letter “X” and is measured in the unit of ohms (Ω).  


Impedance is a comprehensive expression of any and all forms of opposition to electron flow, including both resistance and reactance. It is present in all circuits, and in all components. When alternating current goes through an impedance, a voltage drop is produced that is somewhere between 0^o and 90^o out of phase with the current. Impedance is mathematically symbolized by the letter “Z” and is measured in the unit of ohms (Ω), in complex form.

Impedance Components

The impedance is the general term for the ratio of voltage to current. Resistance is the special case of impedance when φ = 0, reactance the special case when φ = ± 90°.